

Arrays — Understanding the random access
by Deepakumar M, who explains learning in just two words. Hands-on!
Understanding how random access is supported under hood.

Arrays, one of the most predominant data structures that we are using in our day to day programming life. It‘s so popular because of its ease of use and its random access in constant time.
It refers to the ability of a data structure to access all its element in equal time.(i.e) The access time is independent of number of elements in the data structure.


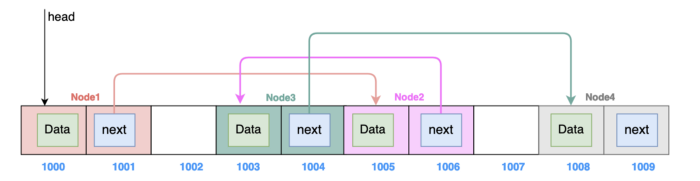
Linked List example
Here in this linked list, we can access the first element in one step using the head reference. Similarly 2 steps for second element, 3 steps for third element and so on. To access any element in the list we need to cross all the elements before it sequentially and so the elements are only sequentially accessible.


Array example
But in arrays, we can directly access any of its indexes — randomly accessible. But how?
For simplicity let’s cover how it is being done in statically typed languages like C, C++, Java etc. In most of these languages we need to explicitly mention the length of the array and the datatype of the elements to be stored in the array. This helps the compilers of the languages to allocate the memory needed during compilation phase itself.
int arr[4]; //Syntax for initializing array in C++.
While compiling this code, the compiler will find a memory location where 10 integers can be stored continuously one after other(contiguous). In terms of size, it will be 16 bytes since the size of integer data type is fixed(4 bytes in C++). Now the compiler points the arr pointer to the starting address of this memory(referred as base address). Let’s assume that the base address is 1000 here and each byte of memory is given a seperate address.


Memory allocation for Array
So when we to try to insert/read data into any random index say 2, with a simple formula we can find the memory location allocated for a particular index.
address = base address + (index * size of one element)
Base Address = 1000
size of each element = 4(bytes)
So the memory location of index 2 will be,
1000 + (4 * 2) = 1008
Since we have got the address, now its the hardware on which we should be able to be directly access any memory location by its address. This is possible in Main memory(RAM) and so we need not worry about that now. So for insert and read operations, it’s just a set of constant time operations:
That implies the time complexity of insert and read operations in an Array to be O(1). But why this is not possible in a linked list?
Let’s visualize the main memory with a 10 bytes of size. Since we are considering byte addressable memory each byte has a unique address.


10 Bytes of main memory(assuming starting address as 1000)
Though the hardware is not built so, trust me — still it is a good idea to visualize main memory in this way. So lets create an array of two integers. At max we can store only 2 elements since to store 3 elements we need 12B(4B each). Say your compiler is allocating 8B starting from address 1000, here’s how our array will be stored in main memory.


Visualizing array in main memoery
Let’s see how it will be stored for a Linked list that contains 5 characters(1B usually). Unlike arrays, the address of a node is only known to its previous node(except head node). So to reach out to a particular node first we need to reach its previous node and so random access is not possible.

Visualizing linked list in main memory
Thus a contiguous allocation is mandatory for Arrays for its random access. Note that the random access in Array is based on the index whereas in data structures like Hash, B Tree, etc. the random access is based on the element itself.
For 2D arrays, we are expected to explicitly mention 3 values — datatype of element to be stored, number of rows, number of columns. Lets consider a 2 x 2 matrix,


Sample 2D array( 2x2 matrix)
Visualizing this in a different way and changing the formula slightly will help us understand how random access is supported in 2D array.


Visualizing a 2D array
Now, here’s the formula for random access in a 2D array(for 0 based indexing):
address = base address + (row number * (size of each row)) + (column number * (size of one element))
Here size of each row is simple as we did for 1D array. Let’s read the element at (0,1).
base address = 1004(assuming as per the image)
row number = 0
size of each row = 8(bytes)
column number = 1
size of one element = 4(bytes)
address = 1004 + (0 * 8) + 1 * 4 = 1008
The address we found from the formula is same as that of in the image and yes the formula works! . Lets check for one more position(1,1).
base address = 1004(assuming as per the image)
row number = 1
size of each row = 8(bytes)
column number = 1
size of one element = 4(bytes)
address = 1004 + (1 * 8) + 1 * 4 = 1016
And again we got it right. Finally this is how random access is supported in 2D arrays. With the little joy of sharing my knowledge on random access, let’s catch up later. Feel free to share your opinions and thoughts over the comments section.
We at CaratLane are solving some of the most intriguing challenges to make our mark in the relatively uncharted omnichannel jewellery industry. If you are interested in tackling such obstacles, feel free to drop your updated resume/CV to careers@caratlane.com!

Leave a Reply